Deep Learning merupakan topik yang sedang nge-trend dikalangan
akademisi ataupun professional. Apa sih Deep Learning itu? Deep
Learning adalah salah satu cabang Machine Learning(ML) yang menggunakan
Deep Neural Network untuk menyelesaikan permasalahan pada domain ML.
Mungkin
nanti akan saya bagi dalam beberapa part. Untuk Part I, kita akan
sama-sama belajar tentang apa itu Neural Network yang merupakan bagian
yang paling penting dari Deep Learning.
Artificial Neural Network
Neural
network adalah model yang terinspirasi oleh bagaimana neuron dalam otak
manusia bekerja. Tiap neuron pada otak manusia saling berhubungan dan
informasi mengalir dari setiap neuron tersebut. Gambar di bawah adalah
ilustrasi neuron dengan model matematisnya.
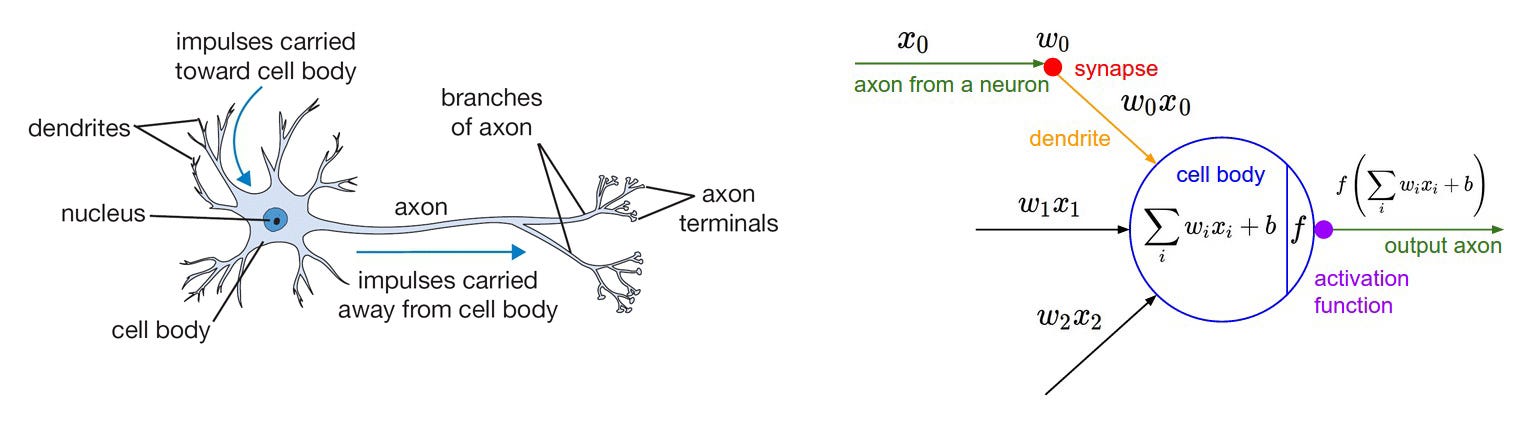
Tiap
neuron menerima input dan melakukan operasi dot dengan sebuah weight,
menjumlahkannya (weighted sum) dan menambahkan bias. Hasil dari operasi
ini akan dijadikan parameter dari activation function yang akan
dijadikan output dari neuron tersebut.
Activation Function
Nah,
mungkin banyak yang bingung apa dan untuk apa activation function?
Sesuai dengan namanya, activation function befungsi untuk menentukan
apakah neuron tersebut harus “aktif” atau tidak berdasarkan dari
weighted sum dari input. Secara umum terdapat 2 jenis activation
function, Linear dan Non-Linear Activation function.
Linear Function
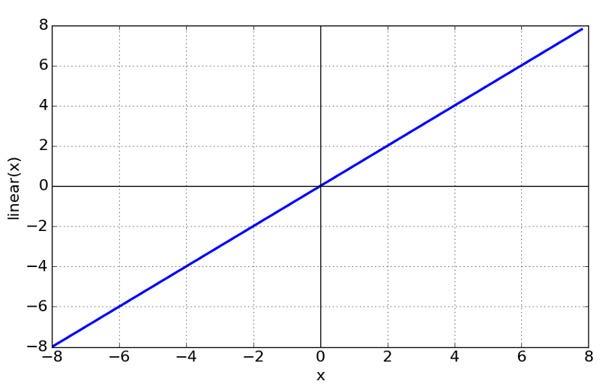
Bisa
dikatakan secara “default” activation function dari sebuah neuron
adalah Linear. Jika sebuah neuron menggunakan linear function, maka
keluaran dari neuron tersebut adalah weighted sum dari input + bias.
Sigmoid and Tanh Function (Non-Linear)
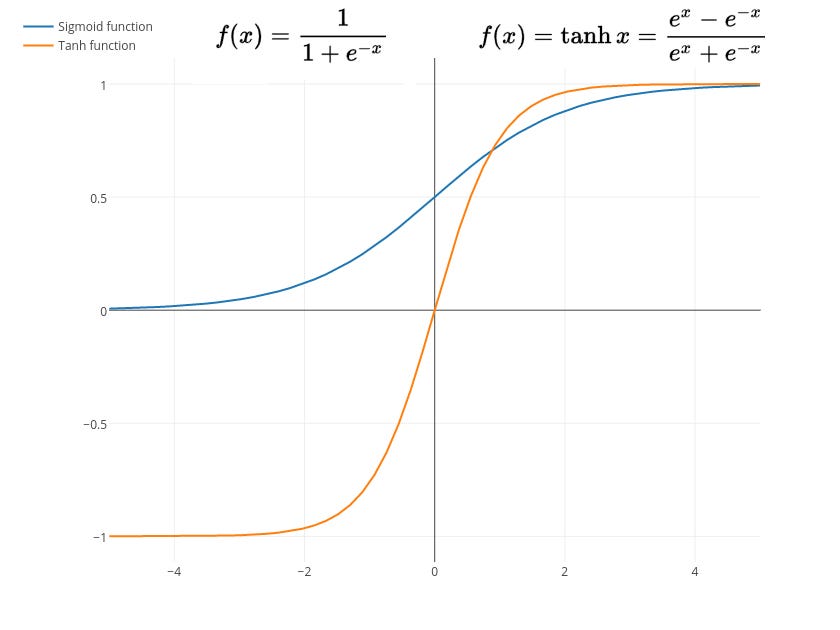
Sigmoid
function mempunyai rentang antara 0 hingga 1 sedangkan rentang dari
Tanh adalah -1 hingga 1. Kedua fungsi ini biasanya digunakan untuk
klasifikasi 2 class atau kelompok data. Namun terdapat kelemahan dari
kedua fungsi ini, nanti akan coba saya jelaskan di part berikutnya.
ReLU (Non-Linear)
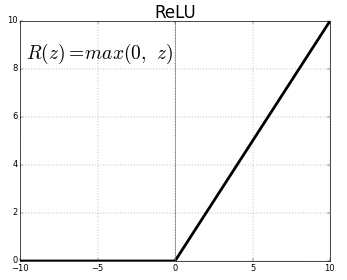
Pada
dasarnya ReLU melakukan “treshold” dari 0 hingga infinity. ReLU juga
dapat menutupi kelemahan yang dimiliki oleh Sigmoid dan Tanh yang nanti
akan saya coba jelaskan di part berikutnya.. :D
Sebenarnya
masih banyak activation function yang lain, namun beberapa fungsi yang
saya sebutkan diatas merupakan fungsi yang sering digunakan. Sebenarnya
masih ada satu lagi Softmax Function, tapi nanti akan saya jelaskan pada
part Multiclass Classification. Untuk referensi lengkap tentang
activation function bisa dibaca di page wikipedia.
Neural Network Architectures
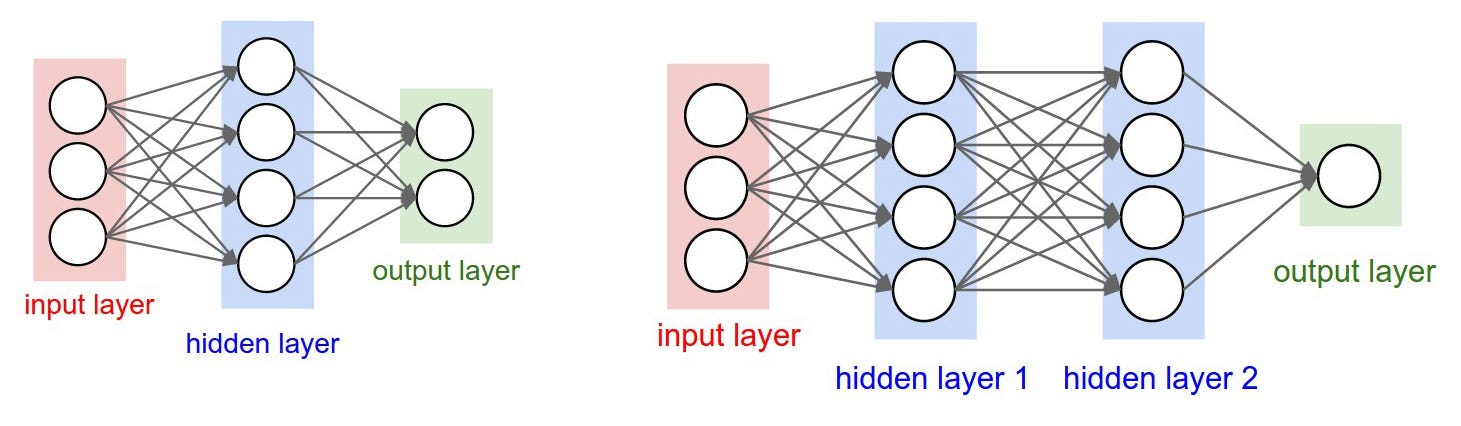
Arsitektur
diatas biasa disebut sebagai Multi Layer Perceptron (MLP) atau
Fully-Connected Layer. Arsitektur pertama mempunyai 3 buah neuron pada
Input Layer dan 2 buah node Output Layer. Diantara Input dan Output,
terdapat 1 Hidden Layer dengan 4 buah neuron. Sedangkan spesifikasi
Weight dan Activation function adalah sebagai berikut:
Weight and Bias
Setiap
neuron pada MLP saling berhubungan yang ditandai dengan tanda panah
pada gambar diatas. Tiap koneksi memiliki weight yang nantinya nilai
dari tiap weight akan berbeda-beda.
Hidden layer dan output layer memiliki tambahan “input” yang biasa disebut dengan bias (Tidak disebutkan pada gambar diatas).
Sehingga
pada arsitektur pertama terdapat 3x4 weight + 4 bias dan 4x2 weight + 2
bias. Total adalah 26 parameter yang pada proses training akan
mengalami perubahan untuk mendapatkan hasil yang terbaik. Sedangkan pada
arsitektur kedua terdapat 41 parameter.
Activation Function
Neuron
pada input layer tidak memiliki activation function, sedangkan neuron
pada hidden layer dan output layer memiliki activation function yang
kadang berbeda tergantung daripada data atau problem yang kita miliki.
Training a Neural Network
Pada
Supervised Learning menggunakan Neural Network, pada umumnya Learning
terdiri dari 2 tahap, yaitu training dan evaluation. Namun kadang
terdapat tahap tambahan yaitu testing, namun sifatnya tidak wajib.
Pada
tahap training setiap weight dan bias pada tiap neuron akan diupdate
terus menerus hingga output yang dihasilkan sesuai dengan harapan. Pada
tiap iterasi akan dilakukan proses evaluation yang biasanya digunakan
untuk menentukan kapan harus menghentikan proses training (stopping
point)
Pada
part selanjutnya, akan saya bahas bagaimana proses training pada neural
network lebih mendalam. Namun pada part ini akan dijelaskan garis
besarnya saja. Proses training terdiri dari 2 tahap :
- Forward Pass
- Backward Pass
Forward Pass
Forward
pass atau biasa juga disebut forward propagation adalah proses dimana
kita membawa data pada input melewati tiap neuron pada hidden layer
sampai kepada output layer yang nanti akan dihitung errornya
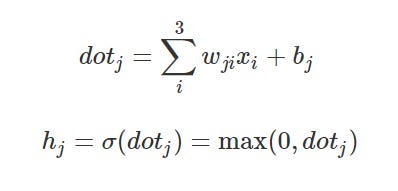
Persamaan
diatas adalah contoh forward pass pada arsitektur pertama (lihat gambar
arsitektur diatas) yang menggunakan ReLU sebagai activation function.
Dimana i adalah node pada input layer (3 node input), j adalah node pada hidden layer sedangkan h adalah output dari node pada hidden layer.
Backward Pass
Error yang kita dapat pada forward pass akan digunakan untuk mengupdate setiap weight dan bias dengan learning rate tertentu.
Kedua
proses diatas akan dilakukan berulang-ulang sampai didapatkan nilai
weight dan bias yang dapat memberikan nilai error sekecil mungkin pada
output layer (pada saat forward pass)
Let’s Code
Pada
bagian ini kita mau mencoba implementasi forward pass menggunakan
Python dan Numpy dulu saja tanpa framework biar lebih jelas. Nanti pada
part-part selanjutnya akan kita coba dengan Tensorflow dan Keras.
Untuk contoh kasusnya adalah kita akan melakukan regresi untuk data yang sebenarnya adalah sebuah fungsi linear sebagai berikut:
f(x) = 3x + 2
Sedangkan arsitektur neural networknya terdiri dari :
- 1 node pada input layer => (x)
- 1 node pada output layer => f(x)
Neural
network diatas sudah saya train dan nanti kita akan melakukan forward
pass terhadap weight dan bias yang sudah didapat pada saat training.
Forward Propagation
Method forwardPass
dibawah ini sangat simple sekali, operasi dot akan dilakukan pada
setiap elemen pada input dan tiap weight yang terhubung dengan input dan
ditambahkan dengan bias. Hasil dari operasi ini akan dimasukkan ke
dalam activation function.
Pre-Trained Weight
Untuk
weight dan bias yang akan kita coba, nilai keduanya sudah didapatkan
pada proses training yang telah saya lakukan sebelumnya. Bagaimana cara
mendapatkan kedua nilai tersebut akan dijelaskan pada part-part
berikutnya.
Kalau dilihat dari weight dan bias diatas, nilai keduanya identik dengan fungsi linear kita tadi :
f(x) = 3x + 2 ≈ f(x) = 2.99999928x + 1.99999976
Complete Code
Pada percobaan kali ini kita akan melakukan perdiksi nilai dari 7, 8, 9 dan 10. Output yang dihasilkan seharusnya adalah 23, 26, 29, 32 dan hasil prediksi adalah 22.99999472, 25.999994, 28.99999328 dan 31.99999256. Jika dilihat dari hasil prediksi, masih terdapat error tapi dengan nilai yang sangat kecil.